How Oppenheimer saved chemistry from quantum mechanics?

Today, we'll see how quantum mechanics questioned the very existence of chemistry as a science and how Oppenheimer, the destroyer of worlds, saved it. You might wonder why this topic should interest you. I suggest this as an answer: this article will show you why it's sometimes worthwhile to overcome fear and dive into topics which seem unapproachable. As an added treat, we'll also touch on the cutting-edge topics in chemistry.

Meta-introduction

Just so you're prepared, this article will feature daunting formulas and equations. This is a deliberate decision; I find it easy to believe in the phrase quoted by Hawking that every equation halves the book sales. While the absence of equations makes articles easier to comprehend, I think that also results in most of the popsci being too superficial (at least to my taste). Let's postpone the question of justifiability of having equations to the conclusion, and for now, let me just tell you what this article is about in a nutshell:

1. We'll start by describing what the reader most likely knows about chemistry and show how the fundamental objectives of chemistry can be formulated as a mathematical problem.
2. I will claim that the best tool for the solution of the postulated problem is quantum mechanics, and I'll share an example of its striking precision.
3. We will introduce two important tools of quantum mechanics: a comprehensive source of information (the wavefunction) and a magic wand (the operator) that will allow us to derive information from the wavefunction.
4. We'll see where the strict quantum mechanics leads and will find that we need to make some audacious assumptions for chemistry to even exist as a science.
5. We'll explore cases when those assumptions break down.
6. Lastly, we will analyze the implications of everything we will learn.

All formulas and equations in the article will play the role of some kind of confirmation of the ideas above. You won't miss anything if you can't understand the formulae; for the purposes of the narrative, it will be more important to see what we do with those formulae, i.e., what approximations we will make. In all cases, I will be clear about what is essential and what is not.

This message is especially significant for high school students: you may be used to being in a situation in which by the time you start to learn a new topic, you are already familiar with all the prerequisites. So, when reading this article, you may think, "well, I need to read more about linear algebra or quantum mechanics before I can read this post". This is a profoundly wrong approach; in real life, you will never be 100% ready, and you will never be able to fulfill all the prerequisites. You just have to be brave and see where curiosity takes you. Shall we?

Part I. Fundamental questions of chemistry

What is chemistry?

What thoughts come to your mind when you hear the word chemistry? Perhaps you think of chemical transformations (combustion of wood, formation of precipitate); maybe you think of chemical formulae (those mysterious $\text{H}_2\text{O}$ or $\text{C}_6\text{H}_6$). Let's focus on the latter. You probably have met the structural representation of molecules (and if you were lucky enough to study organic chemistry, you probably drew them yourself). For example, structures like this:

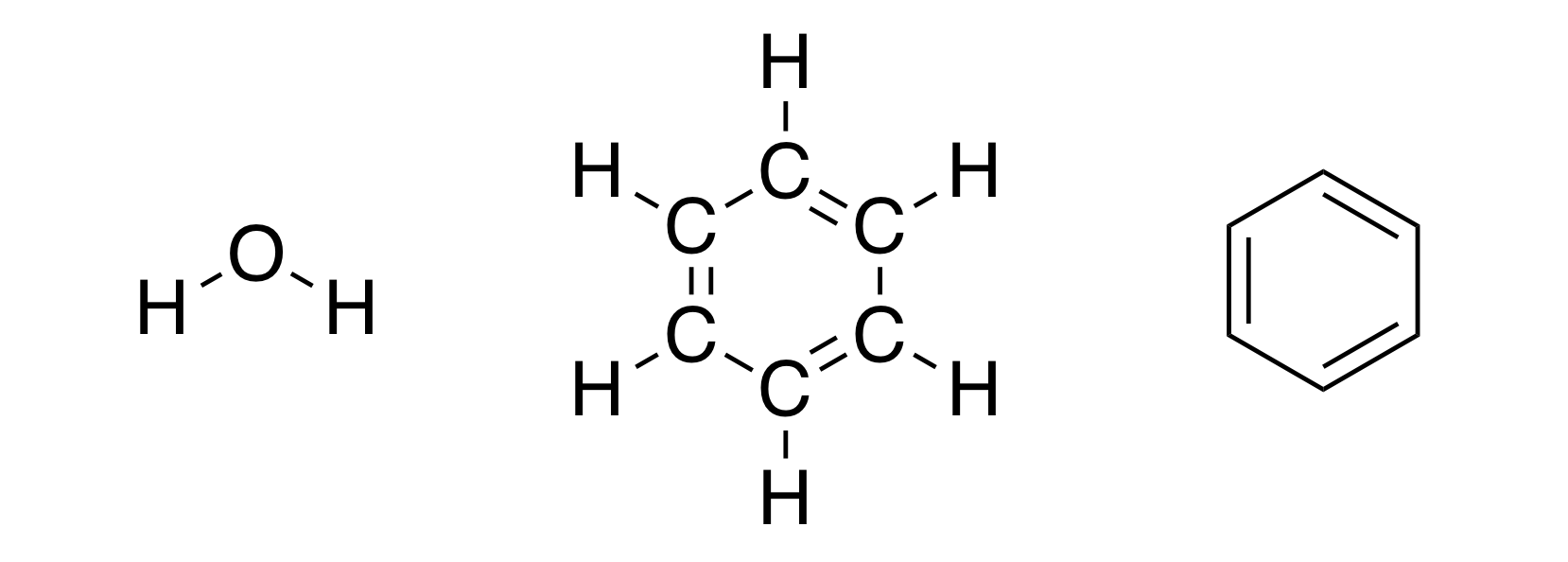
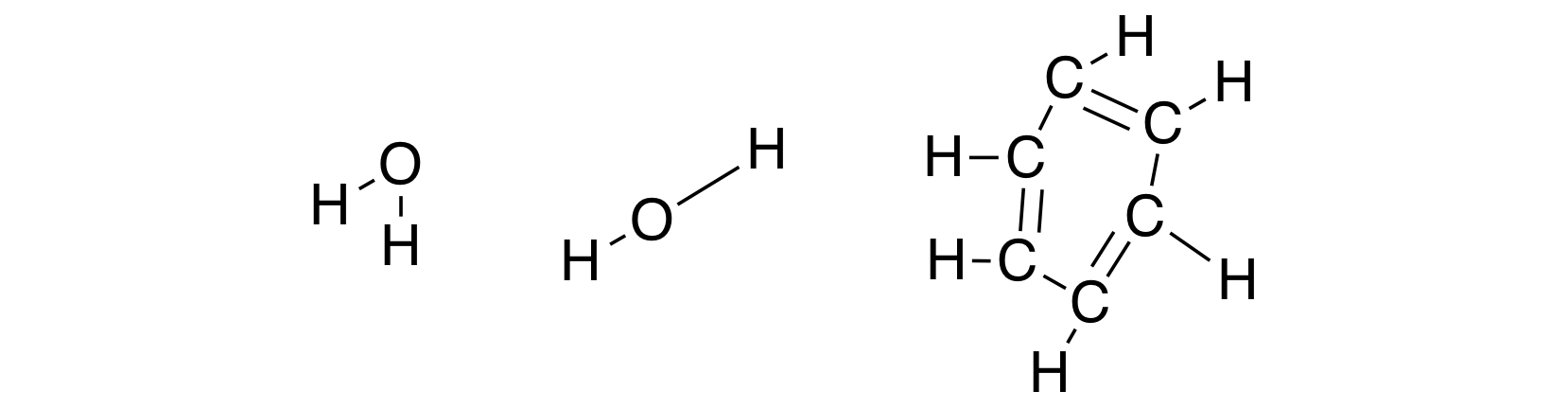
It's peculiar that we sometimes don't realize how much information (in the form of implicit assumptions) can be hidden in a single picture. It may seem that the image above simply shows the structural formulae of water and benzene. But if we think about it, by drawing those molecules in that way, we imply that both oxygen-hydrogen bonds in the water molecule have the same and certain length, that there must be a certain angle between the two O-H bonds. Otherwise, how else can we explain that we draw the structures above and not, for example, the structures below:

But what determines bond lengths and the angle between them? High school chemistry offers the following reasoning: chemical bonds are formed when two atoms share electrons. A Coulomb attraction occurs between the electrons of one atom and the nuclei of the other atom. Simultaneously, there is a Coulomb repulsion among the electrons and among the nuclei. The balance of these two forces determines the equilibrium distances and angles. We can accept this argument, and let's note that we can plot the dependence of the (potential) energy (we will denote it as $V$) on the interatomic distance $R$ for diatomic molecules (you may have already seen this graph).

If we do not limit ourselves to diatomics, we obtain the dependence of the potential energy $V$ on all independent parameters characterizing the structure of the molecule. For example, if we assume both $\text{O-H}$ bonds in a water molecule have the same length, then for an unambiguous description of the water's structure, we need to specify the length of this bond $R$ and the angle between the two bonds (let it be $\theta$). As a result, we get the dependence $V(R, \theta)$, shown in the graph below. We call this surface the potential energy surface (PES). Similar surfaces (called hypersurfaces in multidimensional space) exist for multi-atomic molecules, but visualization becomes difficult as the number of structural parameters increases.

💡 Open this page from a desktop to see interactive figures

The assumptions we make while drawing molecular structures can be formulated as statements describing this surface. For example, this surface must have a minimum, i.e., a point at which the potential energy is minimal¹. The location of this point determines the geometry of our molecule. Thus, the search for the optimal structure of a molecule is reduced to the search for the minimum of a particular function.

Electronic orbitals

Now, let's talk about chemistry as the science of change. A chemical reaction can be described as the process in which chemical bonds break and form. But what creates a chemical bond? Sharing of electrons. And where are electrons located? In orbitals. As part of the school curriculum, you will most likely stop at pictures of atomic orbitals:

The picture above shows, from left to right, top to bottom, the shapes of the $1s, 2s, 2p, 3s, 3p, 4d$ orbitals of the hydrogen atom. By the way, that caveat about the "hydrogen atom" is not accidental at all. It may be surprising, but we know the exact shape of the atomic orbitals (AO) only for the hydrogen atom. We only assume that the shapes of the AOs of other elements are similar to the AOs of hydrogen. Back to our discussion, one might wonder, where are the electrons in molecules? It shouldn't be too shocking to hear that they reside in molecular orbitals (MOs). Molecular orbitals look like this:

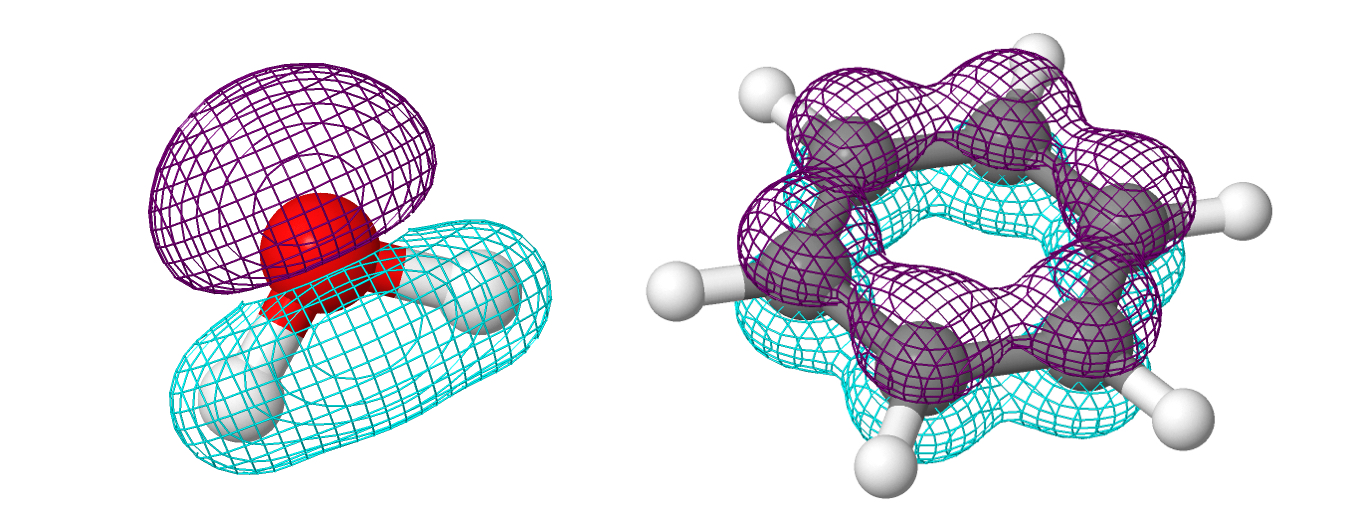
You may wonder how does one find out the shape of MOs? This question is more complicated than it seems. There is no reason why MOs should be similar to AOs, but we feel justified in assuming that they should be similar. Therefore, the primary method for finding the shape of MOs is the so-called Linear Combination of AOs (LCAO method). Simply put, MOs are formed by adding and subtracting AOs with (potentially) different coefficients. The result can be represented in the form of an MO diagram:

Thus, the problem of finding molecular orbitals' shape is reduced to finding the coefficients by which we multiply the AOs before we add them up.

Formalizing fundamental questions in chemistry

We can formulate the ideas described in the two sections above as two fundamental problems of chemistry:

1. Finding the optimal structure of a molecule given the PES. In other words, we know how electrons are attracted to nuclei and repelled from other electrons, and our task is to find such a three-dimensional shape of the molecule that minimizes repulsions and maximizes attractions.
2. Search for optimal molecular orbitals for a particular molecular geometry. The whole procedure of searching MOs described above was conducted for one fixed geometry of the molecule. If we change any of the bond lengths or any of the angles, the MOs will change.

Hold on. The shape of the potential energy surface depends on the interactions of electrons with nuclei and other electrons. These interactions depend on where the electrons are located. However, the arrangement of electrons (their orbitals) depends on how the nuclei are arranged. We get a cyclic dependency. What can we do? For now, we can only state that the problems described above are not independent and, thus, cannot be solved separately.

Part II. The predictive power of quantum mechanics

The most accurate way to describe the structure of atoms (and molecules) is presented by quantum mechanics. But before we move on to using the tools of this theory, it is worthwhile to understand why the scientific community accepts (and maybe even believes in) quantum mechanics. After all, the ideas of corpuscular-wave dualism and substitution of the exact location of electrons in orbits with probability distributions may sound (to put it mildly) questionable.

The accuracy of quantum mechanics

A physical model is correct when it agrees with the experiment (or, even better, can predict its results). The experimental value of the ionization energy of the helium atom is $5\;945\;204\;238(45)$ MHz (the error is given in parentheses). The solution to the Schrödinger equation predicts $5\;945\;262\;288.62(4)$, but this is not the final answer, just a starting point. If we take into account the non-zero size of nuclei, relativistic effects (dependence of mass on velocity), spin-orbit interactions, and polarization of vacuum (using quantum electrodynamics), we have:

As we see, quantum theory predicts the value of energy with, without exaggeration, triumphant accuracy. Even more strikingly, the result of theoretical calculations is limited by the precision with which we know the mass of the helium atom (it is determined experimentally). And we know it with only twelve (12) significant figures. Theory will only take you so far, but one can only envy such so far. The theoretical prediction of the ionization energy is taken from a 2001 paper by Vladimir Korobov and Alexander Elkhovsky.

Part III. Schrödinger equation

One of the most important equations of the quantum theory can be written using four symbols: $\mathcal{{\hat{H}}} \Psi = E \times \Psi$. Here is how you can understand it:

• there is some (mathematical) object that contains all the information about the system (e.g., an atom or a molecule). This is the wave function $\Psi$.
• all physical characteristics we are interested in (including energy $E$) can be obtained by subjecting this source of information to certain transformations through the influence of operators (for example, the Hamiltonian operator $\hat{H}$ if we are interested in energy).

Let's focus on each ingredient individually.

Source of information (wave function)

As we defined above, the wave function is almost a magical object containing information about the system. If we are talking about a molecule, then surely this object must depend on the arrangement of all electrons ($\mathbf{r}$) and nuclei ($\mathbf{R}$). That is, our magic object is a function $\Psi(\mathbf{r}, \mathbf{R})$.

This wave function, which depends on the arrangement of electrons and nuclei, can be decomposed² into an infinite sum of the product of two functions, each of which separately describes either electrons or nuclei:

Where we redefine the function $f_k(\mathbf{R})$ through the sum of functions $h_l(\mathbf{R})$ to have a summation not on two coordinates but on just one. We can understand this equation through the following analogy: $g_k(\mathbf{r})$ and $h_l(\mathbf{R})$ are sort of the simplest elements from which we get the wave function of the whole system using addition (with certain coefficients). If we consider $\Psi$ as a kind of "molecule," the functions $g_k(\mathbf{r})$ and $h_l (\mathbf{R})$ are the constituent "atoms" (mathematicians will call them "basis functions"), and the coefficients $c_{kl}$ show the importance of these "atoms." Further algebraic transformations are done purely for pragmatic purposes.

The decomposition above is exact when $N=\infty$, but it's not hard to guess that working with an infinite set of functions is... a bit hard. It turns out that you can make life a little easier by adding a parametric dependence on $\mathbf{R}$ to $g_k$. What is parametric dependence? It means that depending on $\mathbf{R}$, the shape of the function itself changes. For this arrangement of nuclei, we have this electron arrangement function. And if the nuclei move here, the function becomes different. The end result is:

Where we denote the parametric dependence after the semicolon. This decomposition is still accurate only in the limit $N\to\infty$, but due to this parametric dependence, if we take a finite number of $N$, our accuracy will be slightly higher than before. The function $\psi_k(\mathbf{r}; R)$ is the electron wave function and describes, you won't believe it, electrons. The function $f_k(\mathbf{R})$ represents the rotational and vibrational motions of nuclei.

Transformations to recognize energy

In high school physics, we learn that the energy of a system can be contained in two forms: potential energy and kinetic energy. Similarly, in quantum mechanics, there are transformations (operators) that allow us to find the kinetic energy, and separately, there are operators that enable us to find the potential energy.

Let's try to enumerate forms of energy or interactions found in a diatomic molecule:

• kinetic energy of the first nucleus ($a$)
• kinetic energy of the second nucleus ($b$)
• kinetic energy of electrons (let's denote each one by $i$; there are $n$ in total)
• Coulomb repulsion of nuclei
• Coulomb attraction of electrons to the first nucleus
• Coulomb attraction of electrons to the second nucleus
• Coulomb repulsion of electrons

The total energy must be the sum of these components. Let's write down these energies in the language of quantum mechanics:

where $\mathcal{Z}_a$ and $\mathcal{Z}_b$ are the charges of the nuclei, $M_a$ and $M_b$ are the masses of the nuclei, $e$ is the elementary charge, $R$ is the interatomic distance, and $r_{ai}$ and $r_{bi}$ are the distances from the electrons to the first and second nuclei. The summands on line (5) list the kinetic energies of the two nuclei and all electrons. The summands on line (6) list the potential energies arising from the Coulomb interactions. The complete form of the Hamiltonian operator may frighten you, but I repeat - it is nothing more than the result of translating the list of interactions from English into the language of the mathematical apparatus of quantum mechanics; this means that if you want to be able to reproduce such equations, you will only need to study the English-Quantum Mechanics dictionary.

It is worth dwelling on the mysterious triangles $\Delta_i$ - this is a mathematical operator that finds the rate of change of a function in space. You may already be wondering: change relative to what? The above form assumes the familiar (absolute) coordinate system $(x,y,z)$. It turns out that it is practical to separate the motion of a system (e.g., a molecule) into the motion of its center of mass (which determines the position of the entire molecule) and the relative motions of the components within (e.g., electrons relative to nuclei). To change the coordinate system, it is enough to perform a series of algebraic transformations, and the final result will be:

Things got scarier, but let's try to make sense of it. The first summand in equation (7) is the kinetic energy from the motion of the center of mass. The other summands are grouped into two terms $\hat{H}_0$ and $\hat{H}'$. The former is usually called the electronic Hamiltonian, because it contains the kinetic energy of the electrons (the same $\Delta_i$). $V$ is the same as in equation (5), i.e., it contains all interactions contributing to the potential energy. $\hat{H}'$ contains the kinetic energy from the relative motion of the nuclei ($\Delta_\mathbf{R}$, where $\mathbf{R}$ is the distance between nuclei $a$ and $b$) and the summand $\hat{H}''$ which is responsible for the correlation of the motions of the nuclei and electrons ($\nabla_i$ is another operator, it shows the speed of motion). Grouping summands into $\hat{H}_0$, $\hat{H}'$, and $\hat{H}''$ may not be intuitive, but is nevertheless useful. We will forget about the first summand in equation (7) and will not return to it (we are interested in the internal structure of atoms and molecules, not in how they as a whole move in space).

Part IV. Putting it all together

Let's assemble our ingredients: we have the source of information (the wave function) and the operation (the Hamiltonian operator) that allows us to get the information about the energy. Our wave function:

And our operator:

where recall that $\hat{H}_0$ contains information about the kinetic energy of electrons and Coulomb interactions between electrons and nuclei, the second summand with the triangle is the kinetic energy of nuclei³, and $\hat{H}''$ contains information about the correlation of the motion of nuclei and electrons.

And for completeness of the picture, let's remember the quest for the solutions to which problems led us into quantum mechanics:

1. Search for optimal structural parameters (i.e., values of $\mathbf{R}$): which geometry of the molecule is the most stable?
2. Where are the electrons (i.e., $\mathbf{r}$ values) in the most stable geometry of the molecule?

We also remember that the molecule's stability depends on where the electrons are located; therefore, it is impossible to completely separate the first problem from the second.

Within the mathematical formalism above, the problem reduces to defining the basis (i.e., $g_k(r)$ and $h_l(R)$) and finding the coefficients of $c_{kl}$. Well, we could also find the form of the functions $\psi_k(\mathbf{r}; R) f_k(\mathbf{R})$ for as many values of $k$ as possible (ideally infinite). You may be wondering how you can find the form of a function, and indeed, the problem is challenging. Mathematically, it requires solving the following equation (and this is only for $f_k(\mathbf{R})$):

where $E_k^0$ is the energy obtained due to $\hat{H}^0$, $E$ is the total energy of the molecule, and $\Theta_{kl}$ is the measure of coupling of different energy levels $k$ and $l$.

To make the equation seem even scarier, I will say that some of the operators involve differentiation, and the $\langle \cdot \vert \cdot \rangle$ involves integration, so you are looking at a system of coupled integro-differential equations. We can find $f(\mathbf{R})$ using these equations, but this requires $psi_k$, which must be chosen somehow. We are practically at an impasse, and there is nothing we can do. So that's all for today; thank you all, the structure of molecules is unknowable. Have a good day!

The Born-Oppenheimer Approximation

If the summands $\psi_k$ in the expansion (11) are sufficiently different from each other (which often implies a difference on the energy scale), their coupling can be neglected⁴, and then $\Theta_{kl}=0$ for all $k\neq l$. In this case, the system of equations is greatly simplified since we obtain dependence on only one function $f_k$.

We go further, and say: okay, let our wave function be described by the following product:

In other words, we leave only one term from a decomposition that initially had infinite terms. This form has a very nice intuitive interpretation. The square of the modulus of the wave function can be interpreted as the probability density. Why density? Because if we multiply the square of the modulus by a particular volume of space, we get the probability that there will be a particle in that volume. So then equation (16) says: if you want to know the likelihood that the nucleus is at $\mathbf{R}$ and the electrons are at $\mathbf{r}$, you can first take the probability that the nuclei are at $\mathbf{R}$ and then multiply by the conditional probability that the electrons are at $\mathbf{r}$ given that the nuclei are at $\mathbf{R}$.

It's like the probability that it's raining outside and you're holding an umbrella is the product of the probability that it's raining outside and the conditional probability that you picked up an umbrella if it's raining outside.

We are left with one last step: $E_k^0(\mathbf{R})$ is determined by the kinetic energy of the electrons (which depends on their mass, more precisely $1/m$) and the potential energy, and all terms inside $H_{kk}''(\mathbf{R})$ depend on the mass of the nuclei (more precisely, the $1/M$ or $1/\mu$ dependence). Since atomic nuclei are much (1836 times⁵) heavier than electrons, $H_{kk}''(\mathbf{R})$ will have small values compared to $E_k^0(\mathbf{R})$, and therefore we can neglect it and take $H_{kk}''(\mathbf{R})=0$⁶.

As a result, we get the following equation:

On the right, we have the energy of the system $E$, and on the left, we have two terms. One contains a triangle, so, you might guess, it is related to the kinetic energy. Total energy is made up of kinetic energy and potential energy. So the second summand is potential energy. You may remember that $E_k^0(\mathbf{R})$ came from $\hat{H}_k^0$, which contained information about electrons. A potential energy associated with the location of the electrons?

This is the same potential energy surface or PES we discussed at the very beginning! This is the surface that determines the structure of the molecule! Here, it defines the solution of equation (17), i.e., the function $f_k(\mathbf{R})$, which contains information about the equilibrium (optimal) geometry of the desired molecule.

It is important to note that the very concept of potential energy surface appeared only after we applied the Born-Oppenheimer approximation, the mathematical essence of which is that we took the infinite sum (11) and left only one summand (16). Not having the necessary knowledge of linear algebra, you most likely took steps (3)-(4) for granted, but even so, purely on the intuitive level, it was easier for you to believe that a function can be represented as an infinite sum of other functions than that you can simply take and leave only one term in (16). Whether such a step is justified is a separate question; what is remarkable is that without such an approximation, there will be no potential energy surface. Instead, there will be an infinite sum of such surfaces, each defining different positions of the nuclei. And without a unified surface of potential energy, there is no unified structure.

Otherwise, all we have is a probability distribution of different structures. Just as the electron has no precise orbit around the nucleus and instead obeys a probability distribution of being at a particular point, nuclei have no clear position, only a probability distribution. And so there are no definite chemical bonds; there are no definite lengths of those bonds or angles between them. All we could say about the structure of the benzene molecule $\text{C}_6\text{H}_6$ is that the molecule has spherical symmetry, and the motions of electrons and nuclei are correlated.

We could say roughly the same thing about the structure of a water molecule or a protein molecule. We could try to calculate the average distance between two carbons, but since all carbon atoms are indistinguishable⁷, we would get the average of the distances between any two carbon atoms, not just neighboring ones. Deciphering that the molecule has a flat hexagon shape would probably be impossible.

In fact, given that the true wave function (11) is a sum rather than a single summand, the familiar flat hexagon is no more than one of the shapes taken by the molecule. Some call such a shape a "Born-Oppenheimer structure" to emphasize that its existence is only possible after applying the said approximation. The benzene molecule has at least 217 different structural isomers, i.e., Born-Oppenheimer structures (if stereoisomerism is taken into account, the number rises to 328)⁸. Of these, 17 are acyclic, 71 contain one cycle, 134 two cycles, 87 three cycles, and 19 four cycles. These are structures that satisfy the valence requirements of carbon and hydrogen; unsurprisingly, many of them are unstable. But as many as 80 of them are stable enough to be synthesized, and as many as 40 different variations of the Born-Oppenheimer $\text{C}_6\text{H}_6$ have been synthesized in the lab.

Realize the consequences

Let's repeat it again: without the Born-Oppenheimer approximation, molecules do not have well-defined structures that we are used to drawing in chemistry class. We cannot be sure that a benzene molecule looks precisely as we draw it. In such a case, all the divisions of chemistry that deal with structures of molecules simply become meaningless. For example, organic chemistry is built on drawing two different structures and trying to figure out how to change the bonds so that we can get a product out of a reactant; none of that is possible without having a molecular structure in the first place. Chemistry as a science would not be able to move beyond "there are molecules that have nuclei and electrons, the motions of the nuclei and electrons are highly correlated." In other words, it would simply not exist.

Turns out we are simply lucky that in most situations, the lowest energy term $f_k(\mathbf{R})$ has an energy much lower than the other terms and, therefore, determines the structure of the molecule to a greater extent. However, it is noteworthy that the stability of the summands in the decomposition (11) can vary depending on the chemical environment. For example, benzene on its own prefers to be in the form of a flat hexagon, but if you add steric repulsions, for instance, by replacing three hydrogens with tert-butyl substituents, suddenly the most stable structure is already Dewar's benzene.

Part V. Conic intersections

When we moved from (13) to (15), we assumed that the different terms in the expansion (11) differ sufficiently so that there is practically no coupling between them, i.e., we considered it possible to take $\Theta_{kl}=0$. One may wonder: but what if the different terms are not as well separated? Are there cases when we can't take the coupling to be zero?

There are. We call the different summands in (11) diabatic curves/states. Each of them corresponds to its own potential energy surface. There are points in configuration space¹⁰ where two diabatic curves are close enough to each other and may even intersect. Such intersections are called conical intersections.

💡 Open this page from a desktop to see interactive figures

As you may have guessed, $\Theta_{kl}\neq 0$ and the Born-Oppenheimer approximation breaks down near these conical intersections. For a correct description of these regions of energy hypersurfaces, it is necessary to search for methods of solution of equation (13).

And maybe all this time, you thought that all we are talking about are extremely abstract and exotic concepts that only interest theoretical physicists. And no, conical intersections play a fundamental role in understanding the mechanisms of photochemical reactions. For those familiar with the theory of transition states in organic chemistry - conical intersections in photochemical reactions are like transition states in thermal reactions.

Protein photostability

You may wonder why the primary subjects of modern biology suddenly appear in an article about quantum mechanics. We all know that our Sun, being a fusion reactor, emits some pretty harmful UV rays. You may know that UV rays can break chemical bonds (sometimes this is useful: this is how vitamin D3 biosynthesis occurs). So here's a question for you: what prevents UV radiation from breaking chemical bonds within protein molecules? UV radiation can pass through the phospholipid membrane without any problems, i.e., it definitely reaches proteins. Although the question sounds extremely simple (on the level of "why the sky is blue"), only quantum mechanics can answer it.

The photostability of proteins (and hence of all living organisms) is reduced to the interaction of diabatic states for a hydrogen bond. Suppose that in the ground (initial) state, we have a bond $\text{X}-\text{H}$ and an atom $\text{Y}$ having an unshared electron pair. Between them, there is a hydrogen bond $\text{X}-\text{H}\cdots \text{Y}$. Let us denote this state as $S_0$. Absorption of UV radiation puts the system into the first excited state $^1LE$, near the minimum of which there is a conical intersection with another state $^1 CT$. To this state corresponds another summand in the expansion (11), and hence a different function $\psi(\mathbf{r})$ and $f(\mathbf{R})$. The new $\psi$ function involves a slightly different arrangement of electrons: one electron moves from the $\text{X}-\text{H}$ bond to the $\text{Y}$ atom to form $(\text{X}-\text{H})^+ \cdots \text{Y}^-$, which is called a charge-transfer complex, hence the name CT state. The new function $f(\mathbf{R})$ has a minimum at the point in space where the hydrogen atom is near the atom $\text{Y}$: i.e. $\text{X}^- \cdots (\text{H}-\text{Y})^+$, On the way to the minimum of this state there is another conical intersection, this time with the initial state $S_0$. But in this state, the minimum corresponds to the position of hydrogen closer to the atom $\text{X}$, and the relaxation process is accompanied by a return to square one. The energy that is released as a result of movement along the diabatic curves towards more stable states is dissipated as heat, changing the vibrational states of the surrounding molecules. Simply put, the UV photon energy does not harm chemical bonds and merely heats the water inside the cells.

Notably, the process was described in 2006, i.e., What we are discussing is at the frontiers of human knowledge. If that is not fresh enough for you, here is a remarkable fact. Wave functions have a so-called phase¹¹. The phase of a wavefunction changes during a transition through a conic state. An article published in Nature Chemistry on August 28, 2023 describes an experimental observation of conical intersection on a quantum computer. Four. Weeks. Back.

Conical intersections and DNA

In high school biology, you learn that one of the building blocks of DNA is adenine (systematic name is 6-aminopurine). Have you ever wondered why adenine has this particular structure? Biology has an easy but irrefutable answer: "It's the most evolutionarily advantageous." All right, evolution chose aminopurines. But have you ever wondered why 6-aminopurine and not, say, 2-aminopurine?¹² The main and virtually the only requirement we apply to nucleotide bases in biology is the ability to form hydrogen bonds. But then, 2-aminopurine can form hydrogen bonds with thymine as well as 6-aminopurine does, so we can't establish the reason for choosing the latter.

There's data¹³ to suggest that 6-aminopurine was chosen due to its greater photostability: the lifetime of the excited state (after UV absorption) of 6-aminopurine is a mere 1 picosecond (that's $10^{-15}$ seconds), whereas 2-aminopurine can stay for tenths of a nanosecond (that's $10^{-10}$ seconds). That is, 6-aminopurine reverts to ground state by 5 orders of magnitude or 100,000 times faster. Why do we care how long a molecule spends in an excited state? Because in this excited state, the molecule can engage in photochemical reactions, such as dimerizations, leading to DNA damage (such damage is collectively called DNA lesions). Why is 6-aminopurine able to return to the ground state so much faster? Because it has access to a conical intersection. That is, conical intersection not only helps explain the photostability of DNA, but it also turns out to be the reason¹⁴ why the particular nucleotides were chosen to build DNA.

Part VI. Drawing Conclusions

It's time to look back and reflect on what we learned today:

1. We found that the quest for atomic and molecular structure boils down to searching for the potential energy hypersurface and determining molecular orbitals for the geometry defined by the minimum of that surface.
2. We learned that the tools ($\Psi$ wave function and the $\hat{H}$ operator) of quantum mechanics provide the best solution to the problems above. We started by cataloging the types of interactions within molecules and then rewrote them in the language of the mathematical apparatus of quantum mechanics (5)-(10).
3. We learned that wave functions can be decomposed into an infinite sum of simpler functions (4). We used that expansion to arrive at the grand equation (13)-(14) that allows us to describe the structure of molecules.
4. It turned out that for molecules to simply have a certain three-dimensional structure, we need to make some very bold assumptions (Born-Oppenheimer approximation): to take only one summand from the infinite sum and take some interactions equal to zero.
5. We learned that because there are situations in which this approximation breaks down, UV absorption by proteins and DNA leads to permanent damage less frequently than it might otherwise have had. In other words, conical intersections make our lives possible.

I don't know how the reader feels now, so I'll allow myself to share how I felt when I first learned these topics. It's hard to describe these feelings of simultaneous fear and excitement. Fear of how much you don't know. Excitement that there is so much that is knowable. There are so many questions you don't know the answer to and just as many more to which those answers are yet to be found. And here we come to the discussion of why this article has so many scary formulae.

I don't know how it was for you, but I graduated high school with the feeling that I seemed to understand the general outlines of scientific disciplines, and it remained only to choose one direction for a narrow specialization. Not that I was overconfident (though, who knows, I'm talking about how I remembered myself, not how I really was); it's more like I had no fear from understanding that I knew almost nothing. A fear that appeared about three years ago when I seriously started to delve into quantum mechanics. And personally, it would have been more helpful to me if this fear had appeared earlier. Of course, it's not the fear per se that is useful; it is what it accompanies: the understanding of unexplored expanses of science.

No student in the 11th or 12th grade does not think about what he will do in life. But what kind of careers does he associate with chemistry? Let's just see how many cutting-edge directions we've opened with knowledge from this article:

1. One can take the Born-Oppenheimer structure of a molecule obtained by solving equation (17) and study the electronic structure of that molecule. For example, understanding the energetics of electronic transitions enables the creation of more efficient quantum dots, the semiconductors underlying advanced screens (QLEDs).
2. It can be seen that a chemical reaction is, in fact, no more than a movement along the hypersurface of the potential energy of the system from one point of configurational space to another. Thus, the study of chemical reaction mechanisms is reduced to the study of this hypersurface. In practice, one can search for transition states of reactions of interest and estimate their energy. Repeat the calculations for different structures and thus determine which molecules are worth synthesizing and which are not.
3. It is possible (and necessary) to develop new methods of studying these hypersurfaces. Such quests at times can be reduced to doing pure math. For example, in 2019, a method for finding minimum energy pathways (along which chemical reactions take place) through the search for geodesic curves in Riemannian manifolds was published. In other words, applying the tools of differential geometry has made it possible to do in 5 minutes what used to take days.
4. You can apply the tools of quantum mechanics to the study of biology. If you especially appreciated the mechanism describing the photostability of proteins, you can start studying other examples of proton-coupled electron transfer (PCET). Or you can open the pandora's box of secondary forces affecting protein structure. For example, it turns out that some proteins have $n\to\pi^*$ interactions whose strength is comparable to that of hydrogen bonds. The $n\to\pi^*$ interactions directly result from the shape of molecular orbitals, which are obtained by solving the Schrödinger equation.

When (yes, I hope it is when not if) you start to delve into any of the topics described above, you will suddenly find yourself reading texts that, even though are in English, may seem like are written in alien-ese. There will be many formulae and terminology you have never seen before. You always have a choice in these situations:

1. I don't understand 30/50/70/90% (circle what's appropriate) of the material, so I conclude that I'm not meant to understand it, and I'll stop reading it.
2. I don't understand 30/50/70/90% (circle what's appropriate) of the material, so let me first just take these words/formulae as some abstract object and try to understand what idea/relationship among them this text is trying to build. After one, two, or three passes, I will most likely realize which of these objects are essential and which are given for the sake of completeness. Then, if necessary, I will go and try to study these objects in more detail.

You don't face this dilemma at school because, as a rule, the curriculum is structured to ensure students already know all the prerequisites before a new topic is presented. Personally, I've never experienced a similar feeling of being fully prepared ever after graduating. Perhaps that feeling is only possible at school. Or, said more precisely, when studying STEM, that feeling is only possible at school.

Perhaps the choice you make between the two options above can be a small test of whether you're ready to pursue a career in STEM. Notably, I think that test is sufficient: no matter how much (and what) you know and can do now, if you are willing to wade through previously unknown terms and formulas, then you have what it takes to eventually succeed. And it applies not only to quantum mechanics; if you replace terminology and formulae with molecules and reactions, protein names and regulatory pathways, data structures and algorithms, then I'm sure the same can be said about experimental chemistry, biology, and programming, respectively.

And, if you managed to get to this point in this post, you probably already know what option you prefer to choose. And that means all you have to do is continue to learn and expand your knowledge tree. Everything is possible for you.

P.S. It took 12 hours to format thoughts & contemplations into the first draft of the article. 6.13 more hours to create figures. 5.13 more hours for editing. The article was initially written in Russian (and published through Beyond Curriculum), so 4 more hours for translation & editing. All those hours were spent with amazing score by Ludwig Göransson in the background. I'd like to thank Aray Adylkhan, Bogdan Zagribelnyy, Yernur Kairollayev, Sanzhar Bisenali, and Andrey Tyrin for useful feedback to the first draft of the article.